인공지능을 위한 기초수학 교재를 통해 공부한 내용을 서술하였습니다.
고윳값, 고유벡터, 고윳값 분해
📌 행렬의 선형 변환이란?
행렬 는 벡터에 작용하는 선형 변환입니다.
즉, 어떤 벡터 $v$에 행렬 를 곱하면 새로운 벡터가 됩니다:
$$Av$$
➡️ 예를 들어, 가 다음과 같은 $2 \times 2$ 행렬이라고 해볼게요.
$$ A = \begin{bmatrix}
2 & 1 \\
1 & 2 \\
\end{bmatrix}$$
벡터 $\begin{bmatrix}
x \\ y
\end{bmatrix}$에 대해 행렬 의 변환은:
$$ Av = \begin{bmatrix}
2 & 1 \\
1 & 2 \\
\end{bmatrix}\begin{bmatrix}
x \\ y
\end{bmatrix} = \begin{bmatrix}
2x+y \\ x+2y
\end{bmatrix}$$
➡️ 이렇게 가 벡터의 방향이나 크기를 바꿉니다.
고유벡터, Eigenvector
보통 행렬이 벡터에 작용하면 벡터의 크기와 방향이 모두 바뀜
그런데 어떤 특정한 벡터는 방향은 그대로 두고 크기만 변할 수 있음 👉 고유벡터
$(A - \lambda I)\mathbf{v} = \mathbf{0}$
여기서 $v$는 고유벡터이며, $\lambda$는 고윳값( Eigenvalues ) (벡터의 크기가 변하는 배율)
예제
예를 들어, 다음 행렬 A가 있다고 하면,
$$A = \begin{bmatrix}
2 & 1 \\
1 & 2 \\
\end{bmatrix}$$
벡터 $v = \begin{bmatrix}
1 \\ 1
\end{bmatrix}$는 고유벡터일까?
$$ Av = \begin{bmatrix}
2 & 1 \\
1 & 2 \\
\end{bmatrix}\begin{bmatrix}
1 \\ 1
\end{bmatrix} = \begin{bmatrix}
3 \\ 3
\end{bmatrix}$$
➡️ 이 결과는$ v= \begin{bmatrix}
1 \\ 1
\end{bmatrix}$ 의 크기가 3배 된 상태
➡️ 따라서 $v$는 고유벡터이고, 고윳값은 $\lambda = 3$
고유값과 고유벡터 구하기
고유값 구하기
$\det(A - \lambda I) = 0$
행렬식의 값이 0이 되도록 하는 $\lambda$값을 구하기
고유벡터 구하기
$(A - \lambda I)\mathbf{v} = \mathbf{0}$
구한 고윳값에 대해 위 방정식을 풀어 벡터 v구하기
고유값 분해 , Eigen-decomposition
정방 행렬을 해당 행렬의 고윳값과 고유벡터를 사용해 분해하는 방법
행렬 가 다음과 같은 성질을 가진다고 할 때, 고윳값 분해가 가능
$$(A - \lambda I)\mathbf{v} = \mathbf{0} = \lambda \mathbf{v} $$
➡️ 행렬 는 다음과 같이 고윳값과 고유벡터의 곱으로 분해될 수 있음
$$A = V\Lambda V^{-1} $$
$ A $ → 원래의 행렬
$V$ → 고유벡터로 이루어진 행렬 (각 열이 고유벡터)
$ \Lambda $ → 고윳값이 대각 성분으로 놓인 대각 행렬
$V^{-1}$ → 의 역행렬
📌 고윳값 분해는 왜 하는걸까?
고윳값 분해는 행렬을 다음과 같이 이해할 수 있습니다:
- $\Lambda$ → 대각 행렬 → 크기 조정
- V → 고유벡터 → 좌표축 변환
- $V^{-1}$ → 고유벡터의 변환 해제
➡️ 행렬 의 선형 변환을 고유벡터의 축으로 변환하고, 고윳값에 따라 크기를 조정한 뒤 다시 원래 좌표계로 변환하는 것과 같음!
자세히 설명하자면,
행렬 A가 어떤 벡터에 곱해질 때, 먼저 좌표계를 고유벡터의 축으로 바꿉니다.
즉, 벡터가 고유벡터의 좌표계로 "변환"됩니다.
그 다음, 고유벡터 좌표계에서 크기를 고윳값 만큼 조정합니다.
즉, 특정 방향의 고유벡터에 대해 고윳값만큼 크기가 커지거나 작아집니다.
그리고 고유벡터 좌표계에서의 변환 결과를 다시 원래 좌표계로 되돌립니다.
그렇다면 이걸 왜 하는 걸까!!!!!
👉 변환을 쉽게 하기 위해 좌표계를 바꾸지만,
👉 변환이 끝난 후에는 원래 좌표계에서 결과를 내야 함
예제
행렬 A에 대해 고유값 분해 해보기
$$A = \begin{bmatrix}
4 & 1 \\
2 & 3 \\
\end{bmatrix}$$
Step 1. 고유값 구하기
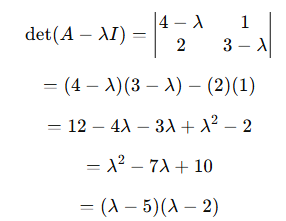
➡️ 따라서 고윳값은 $\lambda_1 = 5 , \lambda_2 = 2$
Step 2. 고유벡터 구하기
- $\lambda_1 = 5$일 때
$(A - 5I)\mathbf{v} = 0$
$\begin{bmatrix}
4-5 & 1 \\
2 & 3-5 \\
\end{bmatrix}\begin{bmatrix}
x_1 \\ x_2
\end{bmatrix} =\begin{bmatrix}
-1 & 1 \\
2 & -2 \\
\end{bmatrix} \begin{bmatrix}
x_1 \\ x_2
\end{bmatrix} = 0$
➡️ $x_1 = x_2$
고유벡터 : $\mathbf{v} = \begin{bmatrix}
1 \\ 1
\end{bmatrix}$ - $\lambda_2 = 2$일 때
$(A - 2I)\mathbf{v} = 0$
$ \begin{bmatrix}
2 & 1 \\
2 & 1\\
\end{bmatrix} \begin{bmatrix}
x_1 \\ x_2
\end{bmatrix} = 0 $
➡️ $x_1 = \frac{-1}{2} x_2$
고유벡터 : $\mathbf{v} = \begin{bmatrix}
-1 \\
2
\end{bmatrix}$
Step 3. 고유값 분해

고윳값 분해의 활용
✔️ PCA (주성분 분석) → 고윳값 분해로 데이터의 주요 축 추출
✔️ 행렬의 지수 연산 (exponential) → 고윳값 분해로 간단해짐
✔️ 양의 정부호 행렬 분해 → 고윳값이 모두 양수일 때 안정적인 계산 가능
✔️ 신경망 훈련 안정화 → Hessian Matrix의 고윳값 분석으로 학습 안정화 가능
'수학' 카테고리의 다른 글
| [AI 수학] 인공지능 수학 - 7. 확률변수와 확률분포 (베르누이, 포아송, 정규분포, 균등분포, 지수분포) (0) | 2025.03.20 |
|---|---|
| [AI 수학] 인공지능 수학 - 6. 기초 통계 (2) | 2025.03.20 |
| [AI 수학] 인공지능 수학 - 4. 기저와 차원, 벡터 공간 (0) | 2025.02.11 |
| [AI 수학] 인공지능 수학 - 3. 선형변환 (0) | 2025.02.11 |
| [AI 수학] 인공지능 수학 - 2. 행렬의 연산과 종류/행렬식 (3) | 2025.02.07 |
