인공지능을 위한 기초수학 교재를 통해 공부한 내용을 서술하였습니다.
확률변수, 확률분포
확률변수, Random variable
일정한 확률을 갖고 발생하는 사건에 수치가 부여되는 함수
즉, 어떤 사건의 결과를 수학적으로 표현하기 위해 사용하는 변수
예를 들어, 동전 2개를 동시에 던지는 시행에서 뒷면이 나오는 동전의 개수를 X라 하면, X에 0, 1, 2를 할당할 수 있음.
➡️ 따라서 X는 확률 변수

X가 가질 수 있는 값의 범위가 이산적인지/연속적인지(셀 수 있는지/없는지)에 따라 이산확률변수와 연속확률변수로 분류 가능
확률분포, Probabilty distribution
확률변수 X가 가지는 $x$에 확률 $P(X = x)$를 대응시키는 함수
어떤 값이 발생할 확률이 어떻게 퍼져 있는지를 나타내는 규칙
즉, 가능한 값들이 얼마나 자주 나오는지를 수학적으로 나타낸 것
| 요소 | 설명 |
| 값 $x$ | 어떤 사건, 수치, 결과 |
| 확률 $P(x)$ | 그 값이 발생할 가능성 |
| 확률분포 $P(x)$ | 가능한 모든 $x$에 대해 확률이 어떻게 퍼져 있는지 |
이산확률변수
변수 X가 취할 수 있는 모든 값 $x$이 취하는 확률이 각각 $f(x_1), f(x_2), .., f(x_n)$로 주어질 때, X를 이산확률변수라고 함
$f(x_i)$를 X의 이산확률함수 또는 확률질량함수라 함
| X | $x_1$ | $x_2$ | ... | $x_n$ | 합(sum) |
| 확률 | $f(x_1)$ | $f(x_2)$ | ... | $f(x_n)$ | 1 |
앞서 언급한 동전 2개를 동시에 던지는 시행에서, 뒷면이 나오는 동전의 개수 X의 확률분포는 아래와 같음

- 이산확률변수 X의 기댓값(평균)과 분산, 표준편차

여러 이산확률분포들
1. 베르누이 분포
베르누이 시행은 1회 시행의 결과가 성공 혹은 실패 두가지 중 하나로만 나오는 실험
성공할 확률이 $p$인 베르누이 시행에서 확률변수 X의 확률분포

이 때, 확률변수 X는 베르누이 분포를 따른다고 하며, $X \tilde{}B(1, p)$로 나타냄
- 기댓값
$E(X) = p$ - 분산
$Var(X) = p * (1-p)$
📌 이항 분포란?
베르누이 시행을 여러 번 반복한 경우의 확률 분포
n번 시행 중 정확히 k번 성공할 확률은
$$P(X = k) = \begin{pmatrix}
n \\ k
\end{pmatrix} p^k(1-p)^{n-k}$$
- 기댓값
$E(X) = n * p$ - 분산
$Var(X) = n * p * (1-p)$
2. 포아송 분포
이항분포 $B(n, p) $에서 평균 $\lambda = np$는 일정하고, n을 한없이 크게 할 때(상대적으로 p는 한없이 작아짐), 이 확률분포는 포아송 분포가 됨
일정 시간이나 일정 공간에서 어떤 사건이 발생하는 횟수가 평균적으로 λ번 발생한다고 할 때, 정확히 k번 발생할 확률은
$$P(X = k) = \frac{\lambda^k e^{-k}}{k!}$$
- 기댓값
$\lambda$ - 분산
$\lambda$
연속확률변수
어떤 범위에 속하는 모든 실수값을 취할 수 있는 확률변수
그 분포는 확률밀도함수를 이용하여 나타냄
연속확률변수 X의 확률밀도함수가 $f(x)$일 때, X가 $a \leq x \leq b$에 있을 확률은 $P(a \leq X \leq b) = \int_{a}^{b} f(x)dx $
확률밀도함수는 확률변수의 분포를 나타내는 함수로, 다음 조건을 만족해야 함

- 연속확률변수 X의 기댓값(평균)과 분산, 표준편차

여러 연속확률분포들
1. 균등분포
연속확률변수 X가 a와 b 사이에서 일정한 값을 취하고 P(a ≤ X ≤ b) = 1일 때,
X는 균등분포(uniformly distribution)를 따른다고 하며, $X \tilde{} U(a, b)$로 표시
모든 값이 동일한 확률로 발생하는 분포
➡️ 균등분포의 확률밀도함수 $f(x)$

모든 값의 발생 확률이 일정하므로 확률 밀도 함수(PDF)는 상수 값

➡️ $X \tilde{} U(a, b)$일 때, 확률변수 X의 기대값과 분산

2. 정규분포
확률변수 X의 확률밀도함수가 다음과 같을 때,
X는 정규분포(normal distribution)를 따른다고 하고 $X \tilde{} N(\mu \sigma^2)$으로 표시
평균을 중심으로 대칭을 이루는 것이 특징
정규분포곡선
정규분포의 확률밀도함수 $f(x)$가 그리는 그래프

- 기댓값
$\mu$ - 분산
$\sigma^2$
✅ 확률변수 X가 정규분포를 따를 때, X가 a 이상 b 이하의 값을 취할 확률은
$$P(a \leq X \leq b) = \int^b_a f(x)dx$$
이때 이것은 바로 아래쪽 그림의 색칠한 부분의 넓이를 의미

3. 지수분포
사건이 서로 독립적일 때, 단위 시간동안 발생하는 사건의 횟수가 푸아송 분포를 따른다면,
다음 사건이 일어날 때까지 대기 시간은 지수분포(Exponential distribution)를 따른다고 함
지수분포의 확률 밀도 함수(PDF)

- = 사건이 발생할 때까지의 시간 간격 (확률 변수)
- = 단위 시간당 평균 발생 횟수 (포아송 분포의 평균 발생률)
- = 자연로그의 밑 (약 2.718)
👉 즉, 평균적으로 시간당 번 사건이 발생할 때, 다음 사건까지 걸리는 시간의 분포가 지수분포

- 기대값 = $\frac{1}{\lambda}$
- 분산 = $\frac{1}{\lambda^2}$
📌 예제 1: 콜센터에 전화가 걸려오는 시간 간격
✅ 콜센터에 전화가 평균적으로 5분에 한 번 걸려온다면, 다음 전화가 10분 안에 올 확률은?
기대값 : $\frac{1}{5}$
다음 사건이 10분 안에 발생할 확률 : $P(X \leq 10)$
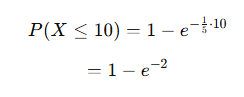
계산하면, 0.8647
👉 따라서 10분 안에 다음 전화가 올 확률은 약 86.5%
'수학' 카테고리의 다른 글
| [AI 수학] 인공지능 수학 - 7. 우도(likelihood)란? (최대가능도/음의 로그 우도) (1) | 2025.04.08 |
|---|---|
| [AI 수학] 인공지능 수학 - 6. 기초 통계 (2) | 2025.03.20 |
| [AI 수학] 인공지능 수학 - 5. 고유값과 고유 벡터, 고윳값 분해 (0) | 2025.03.17 |
| [AI 수학] 인공지능 수학 - 4. 기저와 차원, 벡터 공간 (0) | 2025.02.11 |
| [AI 수학] 인공지능 수학 - 3. 선형변환 (0) | 2025.02.11 |
